Parallel lines m and n are cut by transversal t – Parallel lines m and n, intersected by transversal t, create a fascinating geometric landscape where angles dance in harmony. This intersection unveils a treasure trove of angle relationships and theorems, inviting us to explore the intricate tapestry of parallel lines and transversals.
As we delve deeper into this captivating realm, we will uncover the secrets of alternate interior angles, alternate exterior angles, and corresponding angles. We will unravel the mysteries of the Angle Sum Property and witness the power of the Parallel Line Theorem.
Along the way, we will encounter real-life applications of parallel lines and transversals, from architecture to navigation, showcasing their profound impact on our world.
Parallel Lines and Transversals
In geometry, parallel lines are lines that never intersect, no matter how far they are extended. A transversal is a line that intersects two or more other lines at different points.
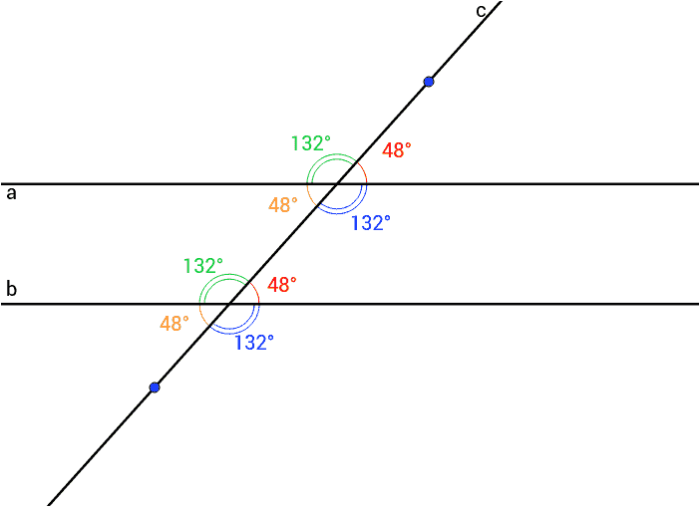
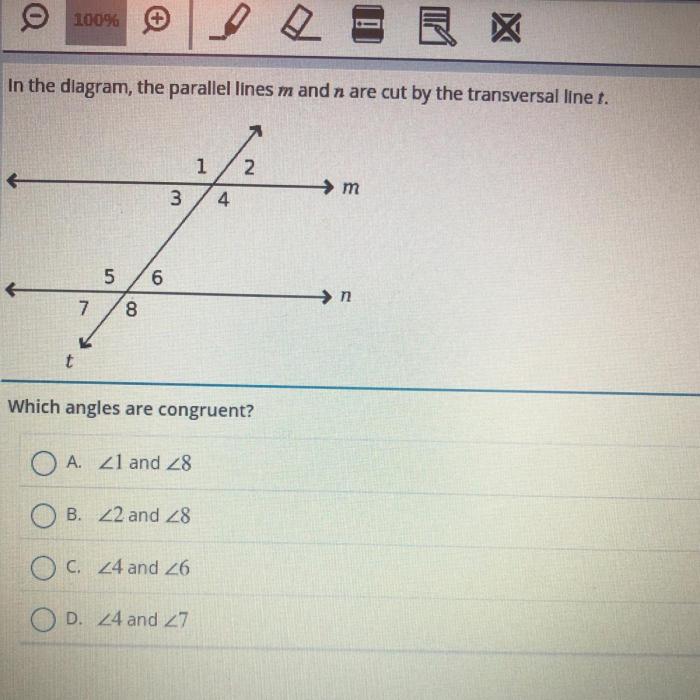
When a transversal intersects two parallel lines, it creates eight angles. These angles are classified into four different types: alternate interior angles, alternate exterior angles, corresponding angles, and consecutive interior angles.
Angle Relationships Formed by Parallel Lines and a Transversal
- Alternate interior anglesare angles that are on opposite sides of the transversal and inside the parallel lines.
- Alternate exterior anglesare angles that are on opposite sides of the transversal and outside the parallel lines.
- Corresponding anglesare angles that are in the same position relative to the transversal and the parallel lines.
- Consecutive interior anglesare angles that are on the same side of the transversal and inside the parallel lines.
The Angle Sum Property for Parallel Lines and a Transversal states that the sum of the measures of the alternate interior angles is equal to 180 degrees. This property can be used to prove that lines are parallel.
Theorems Related to Parallel Lines and a Transversal, Parallel lines m and n are cut by transversal t
The Parallel Line Theorem states that if a transversal intersects two parallel lines, then the alternate interior angles are congruent. This theorem can be used to solve geometry problems involving parallel lines.
The Converse of the Parallel Line Theorem states that if the alternate interior angles formed by a transversal intersecting two lines are congruent, then the lines are parallel.
Applications of Parallel Lines and Transversals
Parallel lines and transversals are used in a variety of applications, including architecture, engineering, and design. For example, parallel lines are used to create the walls of buildings, the beams of bridges, and the tracks of railroads.
Helpful Answers: Parallel Lines M And N Are Cut By Transversal T
What is a transversal?
A transversal is a line that intersects two or more other lines at distinct points.
What is the Angle Sum Property for Parallel Lines and a Transversal?
The Angle Sum Property states that the sum of the interior angles on the same side of a transversal that are formed by two parallel lines is 180 degrees.
What is the Parallel Line Theorem?
The Parallel Line Theorem states that if a transversal intersects two parallel lines, then the alternate interior angles are congruent and the alternate exterior angles are congruent.