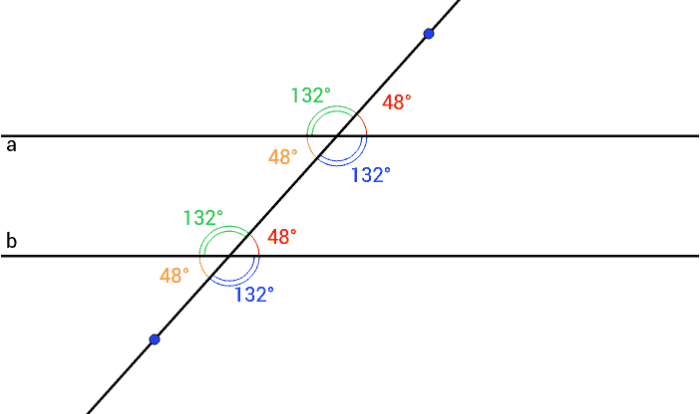
Embarking on unit 10 circles homework 3, we delve into the fascinating world of circles, uncovering their properties, problem-solving techniques, and real-world applications. Join us as we explore the circumference, unravel the mysteries of inscribed and circumscribed circles, and discover the practical significance of circles in engineering and design.
Throughout this journey, we will equip you with a comprehensive understanding of circles, empowering you to tackle problems with confidence and apply your knowledge to real-world scenarios. So, buckle up and let’s dive into the captivating realm of circles!
Concept Review: Circles: Unit 10 Circles Homework 3
A circle is a two-dimensional shape with a constant distance from a fixed point called the center. It is defined by the following properties:
- Radius (r):The distance from the center to any point on the circle.
- Diameter (d):The distance across the circle through the center, which is twice the radius (d = 2r).
- Circumference (C):The distance around the circle, which is approximately 6.28 times the radius (C ≈ 2πr).
Circles have numerous applications in real-world scenarios, including:
- Engineering: Designing wheels, gears, and other circular components.
- Construction: Creating arches, domes, and other curved structures.
- Art and Design: Creating symmetrical and visually appealing patterns.
- Science: Describing the motion of planets, the shape of atoms, and other phenomena.
Problem-Solving Strategies

Circles are versatile shapes with numerous applications in problem-solving. Understanding the properties of circles and developing effective problem-solving strategies can empower you to tackle a wide range of challenges.
Identifying Problem Types
Circle-related problems can be categorized into several types:
- Circumference and Area Calculations:Determining the length of a circle’s circumference or the area enclosed within it.
- Inscribed and Circumscribed Figures:Finding the relationship between a circle and figures inscribed or circumscribed within or around it.
- Tangent Lines:Determining the points of contact and properties of tangent lines drawn to a circle.
li> Arc Length and Sector Area:Calculating the length of an arc or the area of a sector within a circle.
Step-by-Step Problem-Solving Methods
Solving circle-related problems typically involves the following steps:
- Identify the Problem Type:Determine which category the problem falls into (e.g., circumference calculation, inscribed figures, etc.).
- Gather Information:Extract the relevant data provided in the problem statement.
- Apply Relevant Formulas:Use the appropriate formulas or properties of circles to solve for the unknown variables.
- Check Your Answer:Verify the reasonableness of your solution and ensure it aligns with the problem statement.
Worked Examples
Consider the following example:
A circle has a radius of 5 cm. Find its circumference.
Solution:
- Identify the Problem Type:Circumference Calculation.
- Gather Information:Radius (r) = 5 cm.
- Apply Relevant Formula:Circumference (C) = 2πr.
- Check Your Answer:C = 2π(5 cm) = 10π cm ≈ 31.42 cm.
Circle Theorems
Circle theorems are geometric relationships that involve circles. These theorems provide valuable insights into the properties and behavior of circles, making them essential for understanding and solving problems related to circles.
Pythagorean Theorem for Circles
The Pythagorean Theorem for circles states that in a right triangle formed by two tangents to a circle and the radius drawn to the point of tangency, the square of the length of the hypotenuse (the radius) is equal to the sum of the squares of the lengths of the legs (the tangents).
Mathematically, if two tangents to a circle intersect at a point outside the circle, and a radius is drawn to the point of tangency, then:
(Radius)^2 = (Length of Tangent 1)^2 + (Length of Tangent 2)^2
Inscribed and Circumscribed Circles
An inscribed circle is a circle that lies inside a polygon, touching each side of the polygon. A circumscribed circle is a circle that passes through all the vertices of a polygon.
Just finished unit 10 circles homework 3. If you’re looking for a fun and engaging way to learn about the cell, check out tour of the cell chapter 6 . It’s an interactive tour that takes you through the different parts of the cell and explains their functions.
After exploring the cell, I feel more confident about unit 10 circles homework 3.
The properties and applications of inscribed and circumscribed circles are:
- Inscribed Circle:The radius of an inscribed circle is equal to the apothem (the distance from the center of the circle to the side of the polygon).
- Circumscribed Circle:The center of a circumscribed circle is the circumcenter (the point of intersection of the perpendicular bisectors of the sides of the polygon).
- Area and Perimeter:The area of a polygon is equal to half the product of the perimeter of the polygon and the radius of the inscribed circle. The perimeter of a polygon is equal to the sum of the lengths of the sides of the polygon and the radius of the circumscribed circle.
Area and Circumference Calculations
Circles are fundamental shapes in geometry, characterized by their curved perimeter and central point. Understanding the formulas for calculating their area and circumference is crucial for various applications.
The area of a circle represents the region enclosed within its circumference, while the circumference measures the distance around the circle’s perimeter. Both of these measurements are directly related to the circle’s radius, which is the distance from the center to any point on the circle.
Formula Derivation
To derive the formula for the area of a circle, we can imagine dividing the circle into an infinite number of small triangles. The base of each triangle would be a segment of the circumference, and the height would be the radius.
The sum of the areas of all these triangles would be equal to the area of the circle.
Area of a circle = πr²
Where π (pi) is a mathematical constant approximately equal to 3.14159, and r is the radius of the circle.
Similarly, to derive the formula for the circumference of a circle, we can imagine rolling the circle along a straight line. The distance traveled by the circle’s circumference would be equal to the circumference of the circle.
Circumference of a circle = 2πr
Where π (pi) is the same mathematical constant, and r is the radius of the circle.
Relationship between Formulas
The formulas for the area and circumference of a circle are closely related. The circumference is directly proportional to the radius, while the area is proportional to the square of the radius. This relationship highlights the importance of the radius in determining the size and shape of a circle.
Summary Table
For convenience, here is a table summarizing the formulas for different circle measurements:
| Measurement | Formula |
|---|---|
| Area | πr² |
| Circumference | 2πr |
| Diameter | 2r |
Applications in Geometry
Circles play a crucial role in geometric constructions and proofs. They are used to construct angle bisectors, perpendicular bisectors, and other geometric shapes. Circles are also essential in proving triangles congruent and solving geometric problems.
Geometric Constructions
Circles are used in various geometric constructions, such as:
- Angle Bisectors:A circle can be used to construct the bisector of an angle by drawing two arcs from the vertex of the angle that intersect on the opposite side.
- Perpendicular Bisectors:A circle can be used to construct the perpendicular bisector of a line segment by drawing two arcs from the endpoints of the line segment that intersect on a line perpendicular to the line segment.
Geometric Proofs, Unit 10 circles homework 3
Circles are also used in geometric proofs, such as:
- Proving Triangles Congruent:The Inscribed Angle Theorem states that an angle inscribed in a semicircle is a right angle. This theorem can be used to prove triangles congruent.
Solving Geometric Problems
Circles can be used to solve a variety of geometric problems, such as:
- Finding the Area of a Circle:The area of a circle can be found using the formula A= πr2, where ris the radius of the circle.
- Finding the Circumference of a Circle:The circumference of a circle can be found using the formula C= 2 πr, where ris the radius of the circle.
Applications in Real-World Contexts
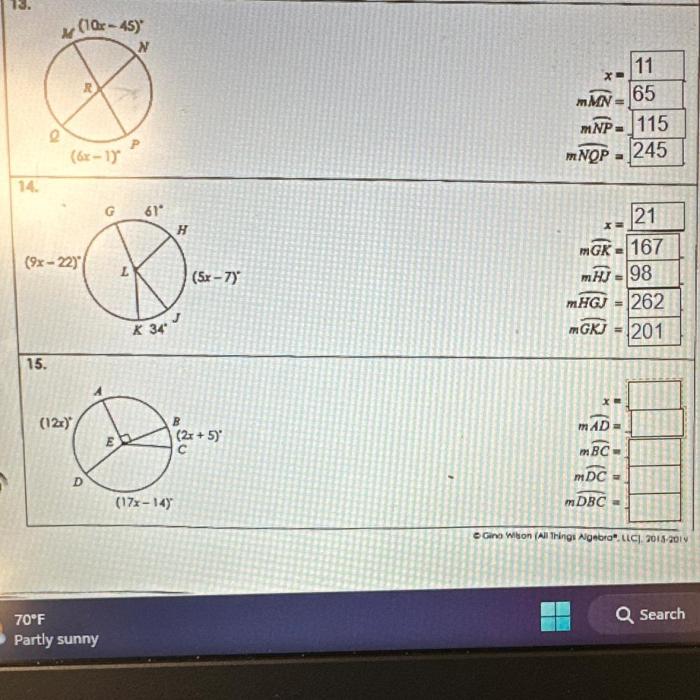
Circles are ubiquitous in our everyday lives, from the wheels on our cars to the gears in our watches. Their unique properties make them essential for a wide range of applications in engineering, design, and other fields.
Engineering and Architecture
Circles are used in various engineering and architectural applications due to their inherent strength and stability. Arches, domes, and bridges utilize circular elements to distribute weight evenly and withstand external forces.
Design and Aesthetics
Circles are often incorporated into designs for their aesthetic appeal and functional benefits. They can create a sense of balance, harmony, and movement in artwork, architecture, and product design.
Measurement and Navigation
Circles play a crucial role in measurement and navigation. Compasses rely on the principle of circular motion to determine direction. Clocks and sundials use circular dials to indicate time.
Transportation
Wheels, gears, and other circular components are essential for transportation. The circular motion of wheels allows vehicles to move smoothly and efficiently. Gears provide mechanical advantage and allow for the transmission of power.
Science and Technology
Circles are used in various scientific and technological applications. Lenses, telescopes, and microscopes utilize circular elements to focus and magnify images. Satellites orbit the Earth in circular paths, providing communication and navigation services.
Frequently Asked Questions
What is the circumference of a circle?
The circumference of a circle is the distance around the circle, calculated using the formula C = 2πr, where r is the radius of the circle.
What is the Pythagorean Theorem for circles?
The Pythagorean Theorem for circles states that in a right triangle inscribed in a circle, the square of the hypotenuse (the diameter of the circle) is equal to the sum of the squares of the other two sides (the radii of the circle).
What is the difference between an inscribed and a circumscribed circle?
An inscribed circle is a circle that lies inside a polygon, touching each of its sides. A circumscribed circle is a circle that passes through all the vertices of a polygon.